Test of independence

Where Is the Independence Test Used in Practice?

In today's era of coronavirus, we see independence tests every day. Every prediction that experts give us is based on this testing. Furthermore, independence testing is used in business, where companies want to know if their marketing efforts, for example, were correct.

In general, the independence test helps in decision-making. It precisely determines whether we have enough data to confirm or refute an assumption.

What Is the Independence Test in Analytics?

The independence test, or chi-square test, measures the expected outcome against the observed result. For example: A principal wants to know when students are most likely to be absent from school. The principal assumes that the chance of student absence is the same every day. He then asks a hundred random colleagues to find out on which days students have the highest absenteeism. The teachers produce the results. The chi-square test then tests whether the opinion of the 100 random teachers is sufficient to confirm or refute the principal's assumption.

Formula for the Independence Test:

χ2 = ∑ (O − E)² / E

E (expectation) expected value

O (observed) observed value

Degree of Freedom

Degree of freedom (DF): DF = (r - 1) * (c - 1)

r (rows) number of cells in the rows of the table

c (columns) number of cells in the columns of the table

How to Conduct an Independence Test?

Define the Null Hypothesis and Alternative Hypothesis
Set the Significance Level
Calculate the Degrees of Freedom
Use the Chi-Square Distribution Table to Determine Critical Values
Perform the Independence Test
The result is the confirmation of the null or alternative hypothesis

1. Define the Null Hypothesis and Alternative Hypothesis

Example:

Null Hypothesis – There is no connection between gender and favorite color among elementary school children

Alternative Hypothesis – There is a connection between gender and favorite color among children

2. Set the Significance Level

The significance level, or Alpha, is determined by you or the researcher.

In most tests, you will encounter a value of 5%.

This is essentially a confidence interval.

Example: If you measure 100 independent data sets and estimate an unknown parameter with a confidence interval, approximately 95 intervals will contain the parameter sought, and about five will not.

3. Calculate the Degrees of Freedom

To calculate the degrees of freedom, use the formula mentioned above.

Degree of freedom (DF): DF = (r - 1) * (c - 1)

r (rows) number of cells in the rows of the table

c (columns) number of cells in the columns of the table

4. Use the Chi-Square Distribution Table to Determine Critical Values

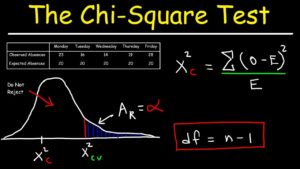
In this step, find the critical value in the table according to your degrees of freedom and significance level. This value will confirm or refute your pre-determined hypotheses.

5. Perform the Independence Test

Now, substitute the values you expected and the values you observed into the formula...